BVE5の相対半径に関する考察(その1)の続きです。
(3)自軌道・他軌道が互いに逆向きの円軌道となる場合
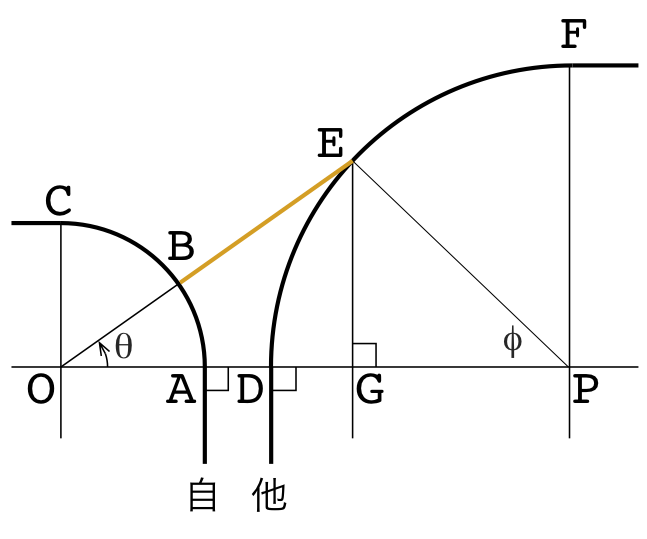
今度は図5に示すような場合を考えます。ここで、自軌道は点Oを中心とする半径\(r_1\)の円軌道、他軌道は点Pを中心とする半径\(r_2\)の円軌道で、これまでと同様\(f(0)=\mathrm{AD}=x_0\)とします。このとき、$$f(l)=\mathrm{BE}=- r_{1} – \sqrt{r_{2}^{2} – \left(r_{1} + r_{2} + x_{0}\right)^{2} \sin^{2}{\left(\frac{l}{r_{1}} \right)}} + \left(r_{1} + r_{2} + x_{0}\right) \cos{\left(\frac{l}{r_{1}} \right)} \quad[8]$$となるので、相対半径は、$$R_c(l)=\frac{r_{1}^{2} \left(\left(- \frac{\left(r_{1} + r_{2} + x_{0}\right) \sin{\left(\frac{l}{r_{1}} \right)}}{r_{1}} + \frac{\left(r_{1} + r_{2} + x_{0}\right)^{2} \sin{\left(\frac{l}{r_{1}} \right)} \cos{\left(\frac{l}{r_{1}} \right)}}{r_{1} \sqrt{r_{2}^{2} – \left(r_{1} + r_{2} + x_{0}\right)^{2} \sin^{2}{\left(\frac{l}{r_{1}} \right)}}}\right)^{2} + 1\right)^{3/2}}{\left(r_{1} + r_{2} + x_{0}\right) \left|{\cos{\left(\frac{l}{r_{1}} \right)} + \frac{\left(r_{1} + r_{2} + x_{0}\right) \left(\sin^{2}\left(\frac{l}{r_{1}} \right)-\cos^{2}{\left(\frac{l}{r_{1}} \right)}\right)}{\sqrt{r_{2}^{2} – \left(r_{1} + r_{2} + x_{0}\right)^{2} \sin^{2}{\left(\frac{l}{r_{1}} \right)}}}- \frac{\left(r_{1} + r_{2} + x_{0}\right)^{3} \sin^{2}{\left(\frac{l}{r_{1}} \right)} \cos^{2}{\left(\frac{l}{r_{1}} \right)}}{\left(r_{2}^{2} – \left(r_{1} + r_{2} + x_{0}\right)^{2} \sin^{2}{\left(\frac{l}{r_{1}} \right)}\right)^{\frac{3}{2}}}}\right|}\quad[9]$$と求められます。(もう少し綺麗に整理できそうな気もしますが、力尽きました・・・)

[9]式のパラメータを具体的に設定すると、図6に示すグラフがプロットできます。この条件で[1]式から求めた相対半径\(\frac{1}{1/300-1/(-200)}\)=120 mなのに対して、[9]式の相対半径は120 mの前後で\(l\)に応じて変動する結果となっています。\(x_0\)の値によっても相対半径が変化することを含め、(2)で考えた配線パターンと類似した傾向を示していると言えます。
[9]式をテイラー展開すると、$$\begin{eqnarray}&R_c(l)&=\frac{r_{1}^{2} r_{2}}{\left(r_{1} + x_{0}\right) \left(r_{1} + r_{2} + x_{0}\right)} \\&&+\frac{\left(r_{1}^{2} \left(- r_{2}^{3} + 4 r_{2}^{2} \left(r_{1} + r_{2} + x_{0}\right) – 3 \left(r_{1} + r_{2} + x_{0}\right)^{3}\right) + 3 \left(r_{1} + x_{0}\right)^{3} \left(r_{1} + r_{2} + x_{0}\right)^{2}\right)}{2 r_{1}^{2} r_{2} \left(r_{1} + x_{0}\right)^{2} \left(r_{1} + r_{2} + x_{0}\right)}l^{2}+ O\left(l^{4}\right)\quad[10]\end{eqnarray}$$が得られます。0次の係数は、\(x_0=0\)の場合に\(\frac{1}{1/r_1+1/r_2}\)となることから、[1]式は\(x_0=0\)での相対半径の0次近似を表しているようです。この点も、(2)での考察と同様の関係が成り立っていると言えます。
(4)自軌道・他軌道が同じ向きの円軌道となる場合
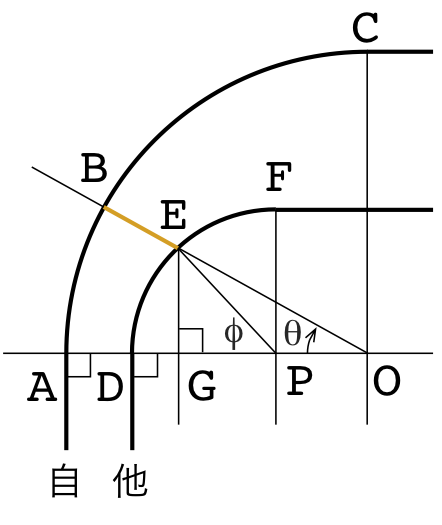
最後に図7のような場合を考えます。これまでと同様に自軌道は点Oを中心とする半径\(r_1\)の円軌道、他軌道は点Pを中心とする半径\(r_2\)の円軌道、\(f(0)=\mathrm{AD}=x_0\)とすれば、$$f(l)=BE=r_{1} – \sqrt{r_{2}^{2} – \left(- r_{1} + r_{2} + x_{0}\right)^{2} \sin^{2}{\left(\frac{l}{r_{1}} \right)}} + \left(- r_{1} + r_{2} + x_{0}\right) \cos{\left(\frac{l}{r_{1}} \right)}\quad[11]$$より、$$R_c(l)=\frac{r_{1}^{2} \left(\left(- \frac{\left(- r_{1} + r_{2} + x_{0}\right) \sin{\left(\frac{l}{r_{1}} \right)}}{r_{1}} + \frac{\left(- r_{1} + r_{2} + x_{0}\right)^{2} \sin{\left(\frac{l}{r_{1}} \right)} \cos{\left(\frac{l}{r_{1}} \right)}}{r_{1} \sqrt{r_{2}^{2} – \left(- r_{1} + r_{2} + x_{0}\right)^{2} \sin^{2}{\left(\frac{l}{r_{1}} \right)}}}\right)^{2} + 1\right)^{3/2}}{\left|{\left(- r_{1} + r_{2} + x_{0}\right) \left(\cos{\left(\frac{l}{r_{1}} \right)} + \frac{\left(- r_{1} + r_{2} + x_{0}\right) \left(\sin^{2}{\left(\frac{l}{r_{1}} \right)}-\cos^{2}{\left(\frac{l}{r_{1}} \right)}\right)}{\sqrt{r_{2}^{2} – \left(- r_{1} + r_{2} + x_{0}\right)^{2} \sin^{2}{\left(\frac{l}{r_{1}} \right)}}}- \frac{\left(- r_{1} + r_{2} + x_{0}\right)^{3} \sin^{2}{\left(\frac{l}{r_{1}} \right)} \cos^{2}{\left(\frac{l}{r_{1}} \right)}}{\left(r_{2}^{2} – \left(- r_{1} + r_{2} + x_{0}\right)^{2} \sin^{2}{\left(\frac{l}{r_{1}} \right)}\right)^{\frac{3}{2}}}\right)}\right|}\quad[12]$$となります。
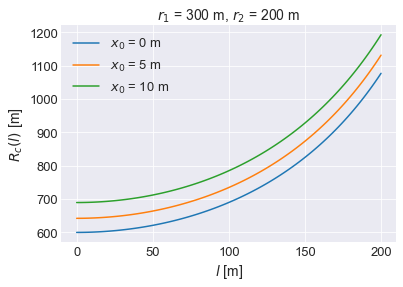
[12]式について具体的なパラメータを設定すると図8のグラフが得られます。[1]式で得られる相対半径\(\frac{1}{1/200-1/300}\)=600 mに対して、\(l\)に応じて単調増加する傾向が見られます。また、(1-3)のパターンに比べて、\(x_0\)が与える影響が大きいことも特徴と言えそうです。
[12]式をテイラー展開すると、\(\left(r_{1} – x_{0}\right) \left(- r_{1} + r_{2} + x_{0}\right) \neq 0\)において$$\begin{eqnarray}R_c(l)&=&\frac{r_{1}^{2} r_{2}}{\left|{\left(r_{1} – x_{0}\right) \left(- r_{1} + r_{2} +x_{0}\right)}\right|} \\ &+& \frac{\left(r_{1}^{2} \left(r_{2}^{3} + 4 r_{2}^{2} \left(r_{1} – r_{2} – x_{0}\right) + 3 \left(- r_{1} + r_{2} + x_{0}\right)^{3}\right) + 3 \left(r_{1} – x_{0}\right)^{3} \left(- r_{1} + r_{2} + x_{0}\right)^{2}\right)}{2r_{1}^{2} r_{2} \left(r_{1} – x_{0}\right) \left|{\left(r_{1} – x_{0}\right) \left(- r_{1} + r_{2} + x_{0}\right)}\right|}l^2+O\left(l^{4}\right)\quad[13]\end{eqnarray}$$が得られます。0次の係数に注目すると、\(r_2>r_1\)かつ\(x_0=0\)の場合に\(\frac{1}{1/r_2-1/r_1}\)となるので、これまでの配線パターンと同様に[1]式は\(x_0=0\)の場合の相対半径の0次近似を表していると考えられます。
マップファイルの試作
以上の結果を基にして、簡単なマップを作ってみました。各曲線の入り口部分のスクリーンショットを図9に示します。本節末尾のリンクからダウンロードできます。
このマップでは、原則として50m毎に配置したTrack構文で、該当する\(f(l), R_c(l)\)により算出したx距離・相対半径を指定しています。相対半径を配線パターンに即して計算することで、座標の指定間隔を広げても歪みの少ない軌道ができると考えていますが、いかがでしょうか?
ただし、よく見ると歪みは残っています。図10は図9右上の部分について他軌道を約5倍ズームした時のスクリーンショットで、軌道が左右に波打っているのが分かります。これは、前記事図4のように変化する相対半径を50m間隔で線形補間する際に生じる誤差が原因と考えられます。少ない座標点で他軌道を表すための最適条件は煮詰める必要がありそうです。
なお、本マップには、ストラクチャーファイルとしてhttps://bvets.net/jp/edit/tutorial/putstructs.htmlにて配布されているstrpack1.zipを同梱しております。strpack1.zipを公開いただいたmackoy氏に感謝いたします。
まとめ
BVE5のTrack構文で使われる「相対半径」について、自軌道距離程の関数として表した他軌道の相対位置\(f(l)\)をもとに、曲率半径\(R_c(l)\)を求めることで考察を試みました。4つの配線パターンについて、得られた曲率半径の0次近似が一般に知られている相対半径の式\(\frac{1}{ 1/R_{他}-1/R_{自}}\)に相当するという結果を得ました。また、得られた\(f(l), R_c(l)\)に基づいてマップファイルを作成し、軌道が概ね想定通りに設定できることを確認しました。
ただし、今回求めた相対半径の式を、このまま実際のマップファイル作成に用いることは困難だと思います。実際の線形は今回考察したパターンよりはるかに複雑であり、手計算で今回求めた4パターンに当てはめていくことには非常な手間がかかると予想できるからです。結局のところ、相対半径には\(\frac{1}{ 1/R_{他}-1/R_{自}}\)式で求めた値を設定して、短い間隔で座標指定を行なっていくことが現実的な手法なのかなと思いました。

