BVE Trainsimの路線マップ作成時に出てくる「相対半径」について、いくつかの配線パターンに対する振る舞いを考えてみました。筆者の数学力はとても褒められたものではないゆえ、厳密さに欠けた部分が多々あるとは思いますが、大目に見ていただければと思います。
注意:本稿は筆者が独自に考察したものであり、BVE Trainsimの公式見解ではありません。本稿の内容に関して、他の方に問い合わせることはご遠慮ください。また、本稿の内容について筆者はいかなる保証もいたしかねますので、あらかじめご承知下さい。
背景
BVEで他軌道の位置を設定するTrack構文では、他軌道の座標に加えて相対半径というパラメータを設定することが必要です。
この相対半径は、\(R_{自}\): 自軌道の半径、\(R_{他}\): 他軌道の半径としたとき、$$\frac{1}{ 1/R_{他}-1/R_{自}} \quad[1]$$式で求められることが一般に知られていますが、いざこの式を使って相対半径を設定すると思った通りにならないことがあり、困っていました。
そんな折、Mi5000氏の以下のツイートを発見し、他軌道の相対位置を関数として定義できれば、曲率半径を導出することで相対半径が解析的に理解できるのでは?、という発想に至りました。
相対半径の定義
まず、自軌道と他軌道の関係を整理します。自軌道上の距離程lでの位置を点Pとするとき、点Pでの自軌道の接線と法線は図1のように表されます。自軌道接線の方向は距離程lでの自列車の進行方向に相当し、点Qを自軌道法線と他軌道の交点とすれば、線分PQの長さが注目する他軌道のx方向位置となります。
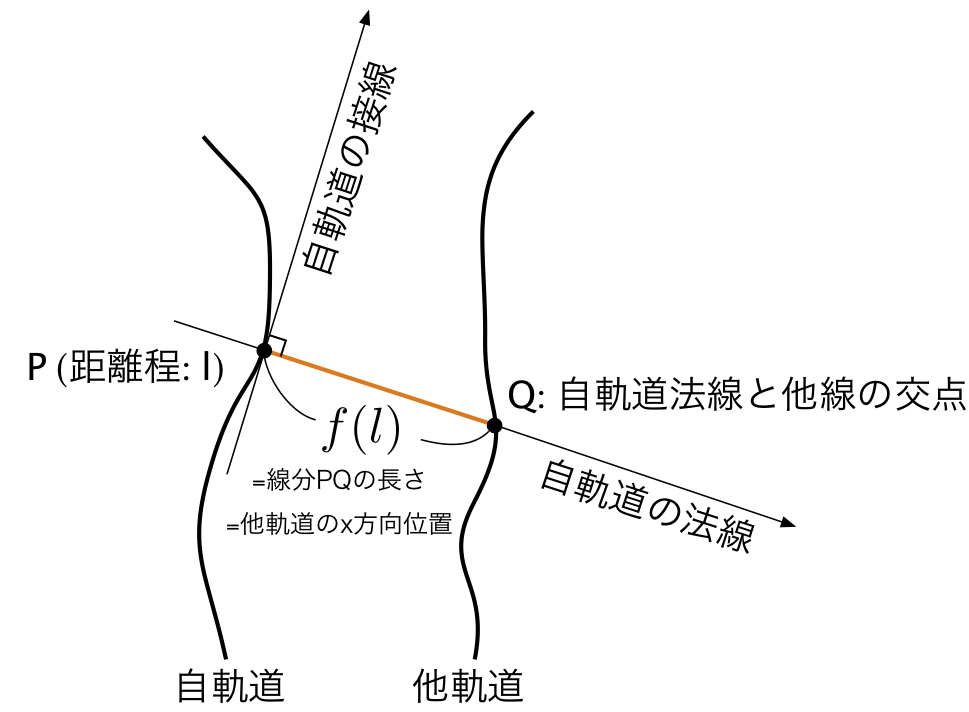
ここで、線分PQの長さを距離程\(l\)の関数として\(f(l)\)で表せば、\(f(l)\)は自軌道に対する他軌道の相対的な線形を表す関数に相当します。本稿では、関数\(f(l)\)の曲率半径\(R_\mathrm{c}(l)\)を、BVE5における他軌道の相対半径として考えます。なお、曲率半径\(R_\mathrm{c}(l)\)は、\(l\)での\(f(l)\)の曲率の逆数として、$$R_\mathrm{c}(l)=\frac{\left(1+\left(\frac{df}{dl}\right)^2\right)^{3/2}}{\left|\frac{d^2f}{dl^2}\right|} \quad[2]$$で表されます。
本稿では簡単化のため、自軌道、他軌道ともにy方向の座標は変化しない場合を考えます。同様に簡単化のため、単一Rで表される曲線のみを考え、緩和曲線や複心曲線のような途中でRが変化する線形はとりあえず考えません。
(1)自軌道が直線、他軌道が曲線の場合
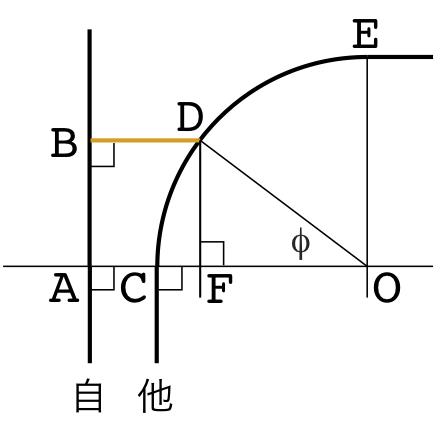
簡単そうなパターンとして、まず図2のような直線の自軌道に対して他軌道が円軌道で離れていく線形を考えます。直線ABを自軌道とし、線分ABの長さで距離程\(l\)を表すこととします。他軌道は半径\(r_1\)の点Oを中心とする弧CEで表されるとし、\(l=0\)での軌道間隔(=線分ACの長さ)を\(x_0\)とします。
このとき、他軌道の相対位置\(f(l)\)は、点Bにおける自軌道の法線と他軌道の交点Dの距離BDで表すことができます。\(\angle \mathrm{DOC}=\phi\)として、点DからAOに下ろした垂線の交点をFとするとき、$$\mathrm{BD} = \mathrm{AC}+\mathrm{CF}, \\ \mathrm{AB} = \mathrm{DF} = r_1\sin\phi \\ \mathrm{CF}=r_1(1-\cos\phi)$$なので、$$f(l)=x_0+r_1\left(1-\sqrt{1-\left(\frac{l}{r_1}\right)^2}\right) \quad[3]$$と求められます。従って相対半径\(R_\mathrm{c}(l)\)は、$$R_\mathrm{c}(l)=r_1 \quad[4]$$となり、\(l,x_0\)によらず他軌道の円半径と同一の値をとることが分かります。なお、ここで求めた\(f(l), R_\mathrm{c}(l)\)は、\(|l|\le r_1\)の範囲でのみ成り立つことに留意してください。
(2)自軌道が曲線、他軌道が直線の場合
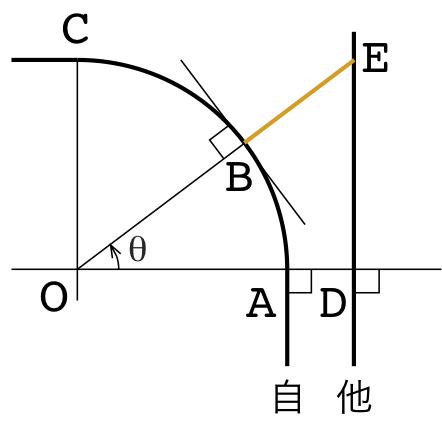
次に(1)とは逆のパターンとして、図3のような場合を考えます。ここでは、自軌道を半径\(r_1\)の点Oを中心とする円弧ACとし、弧ABの長さで距離程\(l\)を表します。他軌道は直線DEで表されるとし、(1)と同様に\(f(0)=\mathrm{AD}=x_0\)とします。
他軌道の相対位置\(f(l)\)は、点Bにおける自軌道の法線と他軌道の交点Eの距離BEに相当します。\(\angle \mathrm{AOB}=\theta\)とすれば、$$\mathrm{OE}\cos\theta = \mathrm{OA}+\mathrm{AD} = r_1 + x_0, \\ l =\stackrel{\frown}{\mathrm{AB}} = r_1\theta, \\ \mathrm{BE} = \mathrm{OE}-\mathrm{OB} $$より、$$f(l)=\frac{r_1+x_0}{\cos\frac{l}{r_1}}-r_1 \quad[5]$$と求められます。これより、相対半径は$$R_\mathrm{c}(l)=\frac{\left(r_{1}^{2} \cos^{4}{\left(\frac{l}{r_{1}} \right)} + \left(r_{1} + x_{0}\right)^{2} \sin^{2}{\left(\frac{l}{r_{1}} \right)}\right)^{3/2}}{r_{1} \left(r_{1} + x_{0}\right) \left(\sin^{2}{\left(\frac{l}{r_{1}} \right)} + 1\right) \left|{\cos^{3}{\left(\frac{l}{r_{1}} \right)}}\right|} \quad[6]$$となり、距離程\(l\)の関数であることがわかりました。なお、導出にはSymPyを利用しました。
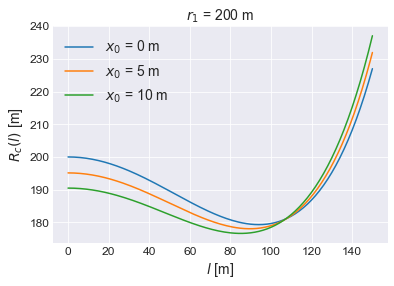
[6]式の振る舞いを調べるため、具体的なパラメータを与えてグラフを作ってみます。図4は、自軌道半径\(r_1\)=200 mでの相対半径を、原点での軌道間隔\(x_0\)=0, 5, 10 mの場合についてプロットしたものです。[1]式で求められる相対半径は200 m (=\(r_1\))であるのに対し、[6]式の値は\(l\)に応じて複雑に変動することと、\(x_0\)の値によっても変化することが見て取れます。
[1]式との関係を調べるため、[6]式をテイラー展開してみます。2次の項まで展開すると、$$ R_\mathrm{c}(l)=\frac{r_{1}^{2}}{r_{1} + x_{0}} + l^{2}\left( \frac{ -1 + 3\frac{ x_{0}}{r_{1}} + 1.5\frac{ x_{0}^{2}}{r_{1}^{2}}}{r_{1} + x_{0}} \right) + O\left(l^{4}\right) \quad[7]$$が得られます。0次の項は\(x_0=0\)で\(r_1\)となることを考えると、[1]式は\(x_0=0\)の場合の相対半径を0次近似したものと言えそうです。
その2へつづきます。